如果一個棱錐的底面是正多邊形，且頂點在底面的射影是底面的中心，這樣的棱錐叫正棱錐。 特別地，側棱與底面邊長相等的正三棱錐叫做正四面體。

正棱錐基本性質：

（1）正棱錐各側棱相等，各側面都是全等的等腰三角形，各等腰三角形底邊上的高相等（它叫做正棱錐的斜高）；

（2）正棱錐的高、斜高和斜高在底面內的射影組成一個直角三角形，正棱錐的高、側棱、側棱在底面內的射影也組成一個直角三角形；

（3）正棱錐的側棱與底面所成的角都相等；正棱錐的側面與底面所成的二面角都相等；

（4）正棱錐的側面積：如果正棱錐的底面周長為c，斜高為h，那么它的側面積是 s=1/2ch。

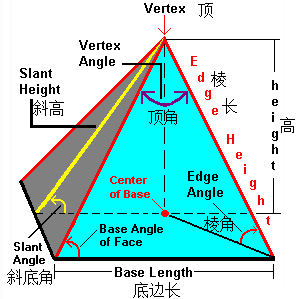
上面的圖形為正多棱錐，它的底邊是正多邊形，它的側面全部為全等的等腰三角形，同時，它的頂點垂直于底面。

使用示例

輸入數據：

正棱錐邊數：5；底邊長：4；高：6

點擊“計算”，輸出數據

體積：55.055；體面積：27.528；

斜高：6.6013；棱長：6.8977；

底面角：73.145；頂角：33.71；

斜角：65.355；棱角：60.442；

側面積：13.203；側面積和：66.013；

總面積：93.541；側面周長：17.795；

底面周長：20；底內角：108；

底內角和：540；底外角：72；

底中心角：72；外接圓半徑：3.4026；

內切圓半徑：2.7528