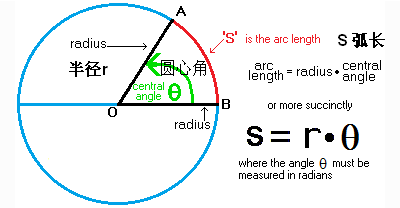
弧長公式：\(l=(nπr)/180\)或\(l=n/180·πr\)或\(l=|α|r\)

• n是圓心角度數，
• r是半徑，
• α是圓心角弧度。

在半徑是R的圓中，因為360°的圓心角所對的弧長就等于圓周長\(C=2πR\)，所以n°圓心角所對的弧長為\(l=(n°πR)/180°\)

在弧度制下，若弧所對的圓心角為θ，則有公式L=Rθ。扇形面積公式S=LR/2,相對應的則有扇形面積計算公式\(S=RRθ/2\)

在圓中，連接圓心和圓上任意一點的線段叫做圓的半徑。通常用字母r來表示。

圓心角頂點在圓心上，角的兩邊與圓周相交的角叫圓心角。圓心角∠AOB的取值范圍是0°＜∠AOB＜360°

使用示例

輸入數據：

計算弧長

半徑：5

圓心角（弧度）：45

點擊“計算”，輸出數據

弧長等于：225